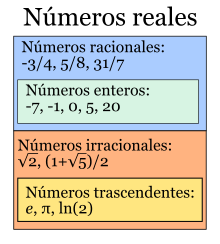
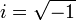Análisis de errores:
Análisis de errores
Corriente de investigación que se desarrolló
durante los años 70 del siglo XX como una rama de la Lingüística aplicada.
Se proponía el estudio y análisis de los errores cometidos por los aprendientes de segundas lenguas para descubrir sus
causas y conocer las estrategias que utilizan los alumnos en el proceso de aprendizaje.
El análisis de errores surgió como alternativa al análisis contrastivo.
En 1967 S. P. Corder presentó uno de los artículos fundacionales de esta
corriente«The significance of learner's errors». Hacia finales de los años 70
del siglo XX, la teoría evolucionó hacia los estudios de la interlengua y la adquisición de segundas lenguas.
A diferencia del análisis contrastivo, el método
seguido por el análisis de errores no partía de la comparación de la lengua
materna y la lengua meta del aprendiente, sino de sus producciones reales en
lengua meta; tomando éstas como punto de partida, se procede mediante los
siguientes pasos, recomendados en 1967 por S. P. Corder:
- Identificación de los errores en su contexto;
- clasificación y descripción de los mismos;
- explicación de su origen, buscando los mecanismos
o estrategias psicolingüísticas y las fuentes de cada error: en este punto
entra la posible interferencia de la
lengua materna, como una estrategia más;
- evaluación de la gravedad del error y búsqueda de un posible tratamiento.
Como consecuencia de estos estudios, se observó
que los errores reflejaban estrategias universales de aprendizaje. De ahí nace
la aportación más importante de esta corriente: el cambio de visión del error.
Los errores empezaron a ser considerados como un factor provechoso en el
aprendizaje porque constituían un paso ineludible en el camino de
apropiación de la nueva lengua y eran valorados como índices de los
diversos estadios que el aprendiente atraviesa durante el proceso de aprendizaje. De esta
última asunción se pasaría al concepto de interlengua.
Desde un punto de vista psicolingüístico, esta
corriente se apoyaba esencialmente en las investigaciones realizadas en los
trabajos de N. Chomsky (1965) sobre la adquisición de la lengua materna. En
esta teoría, la adquisición se concibe como un proceso creativo del niño, el
cual, sirviéndose de un dispositivo interno, es capaz de construir la gramática
de su lengua materna a partir de los datos a los que está expuesto. Siguiendo
este planteamiento, se esperaba un proceso análogo en la adquisición de la
segunda lengua.
El análisis del error se
ha planteado del siguiente modo: por un lado, se han analizado las
distintas bases
cartográficas disponibles para ejecutar el programa (en busca del error
inherente) y, por otro,
se ha tratado de expresar el error de truncamiento que se deriva de la
modelización que el
programa realiza del trazado, en función de la información cartográfica.
El error inherente es muy difícil de determinar con
exactitud, si bien suele ser un error
pequeño; por este
motivo, el error de truncamiento se ha calculado independientemente de
los posibles errores de
la base cartográfica utilizada.
Todas las medidas
experimentales vienen afectadas de una cierta imprecisión inevitable debida
a las imperfecciones del
aparato de medida, o a las limitaciones impuestas por nuestros sentidos que deben
registrar la información.
El principal objetivo de
la denominada teoría de errores consiste
en acotar el valor de dichas imprecisiones, denominadas errores experimentales. Dado que el valor de las magnitudes
físicas se obtiene experimentalmente por medida (bien directa de la magnitud o
bien indirecta, por medio de los valores medidos de otras magnitudes ligadas
con la magnitud problema mediante una fórmula física) debe admitirse como
postulado físico el hecho de que resulta imposible llegar a conocer el valor
exacto de ninguna magnitud, ya que los medios experimentales de comparación con
el patrón correspondiente en las medidas directas, viene siempre afectado de imprecisiones
inevitables. De este modo, aunque es imposible encontrar en la práctica el
valor "cierto" o "exacto" de una magnitud determinada, no
hay duda de que existe, y nuestro problema es establecer los límites dentro de
los cuales se encuentra dicho valor.
CLASIFICACIÓN DE LOS
ERRORES
El error se define como
la diferencia entre el valor verdadero y el obtenido experimentalmente.
Los errores no siguen
una ley determinada y su origen está en múltiples causas. Atendiendo a las causas
que los producen, los errores se pueden clasificar en dos grandes grupos,
errores sistemáticos y errores accidentales.
Error sistemático: es aquel que es
constante a lo largo de todo el proceso de medida y, por tanto, afecta a todas
las mediciones de un modo definido y es el mismo para todas ellas. Estos errores
tienen un signo determinado y las causas probables pueden ser las siguientes:
- Errores instrumentales (de aparatos). Por ejemplo el error
de calibrado es de este tipo.
- Error personal.
Este es, en general, difícil de determinar y es debido a limitaciones de
carácter
personal. Un ejemplo de
éste sería una persona con un problema de tipo visual.
- Error de la elección del
método. Corresponde a una elección inadecuada del método de medida
de la magnitud. Este tipo de error puede ponerse de manifiesto cambiando el
aparato de medida, elobservador, o el método de medida.
Se denominan errores accidentales: a aquellos que se producen en las pequeñas variaciones
que aparecen entre
observaciones sucesivas realizadas por un mismo operador. Las variaciones no son
reproducibles de una medición a otra, y no presentan más que por azar la misma
magnitud en dos mediciones cualesquiera del grupo. Las causas de estos errores
son incontrolables para un observador. Los errores accidentales son en su
mayoría de magnitud muy pequeña y para un gran número de mediciones se obtienen
tantas desviaciones positivas como negativas. Aunque con los errores
accidentales no se pueden hacer correcciones para obtener valores más
concordantes con el real, si se emplean métodos todos estadísticos se puede
llegar a algunas conclusiones relativas al valor mas probable en un conjunto de
mediciones.
CONCEPTOS DE EXACTITUD,
PRECISIÓN Y SENSIBILIDAD
En lo que respecta a los
aparatos de medida, hay tres conceptos muy importantes que vamos a
definir exactitud,
precisión, y sensibilidad.
La exactitud se define como el grado de concordancia entre el valor
verdadero y el experimental. De modo que, un aparato es exacto si las medidas
realizadas con él son todas muy próximas al valor "verdadero" de la
magnitud medida.
La precisión hace referencia a la
concordancia entre una medida y otras de la misma magnitud,
realizadas en
condiciones sensiblemente iguales. De modo que, un aparato será preciso cuando
la diferencia entre diferentes medidas de una misma magnitud sea muy pequeña.
La exactitud implica
normalmente precisión, pero la afirmación inversa no es cierta, ya que
pueden existir aparatos
muy precisos que posean poca exactitud debido a los errores sistemáticos tales
como error de cero, etc. En general, se puede decir que es más fácil conocer la
precisión de un aparato que su exactitud.
La sensibilidad de un aparato está relacionada con
el valor mínimo de la
magnitud que es capaz de
medir. Por ejemplo, decir que la sensibilidad de una balanza es de 5 mg significa
que para masas inferiores a la citada, la balanza no presenta ninguna
desviación.
Normalmente, se admite
que la sensibilidad de un aparato viene indicada por el valor de la
división más pequeña de
la escala de medida. En muchas ocasiones, de un modo erróneo, se toman como
idénticos los conceptos de precisión y sensibilidad, aunque hemos visto ya que
se trata de conceptos diferentes
ERROR ABSOLUTO. ERROR
RELATIVO
Si medimos una cierta
magnitud física cuyo valor "verdadero" es x0, obteniendo un valor de la
medida x, llamaremos error absoluto en dicha medida, a la
diferencia:
Δx = x – x0
donde en general se
supone que |Δx| << |x0|.
El error absoluto nos da una medida de la desviación, en
términos absolutos respecto al valor "verdadero". No obstante, en
ocasiones nos interesa resaltar la importancia relativa de esa desviación. Para
tal fin, se usa el error relativo.
El error relativo: se define como el cociente entre el error absoluto y el
valor "verdadero":
ε =Δx
/ x0
En forma porcentual se
expresará multiplicado por cien. Cuando indiquemos el valor de una medida de
una magnitud, tendremos que indicar siempre el grado de incertidumbre de la
misma, para lo que acompañaremos el resultado de la medida del error absoluto
de la misma, expresando el resultado en la forma:
x ± Δx
De ordinario, y dado el
significado de cota de imprecisión que tiene el error absoluto, éste
jamás debe tener más de
dos cifras significativas,
admitiéndose por convenio, que el error absoluto sólo puede darse con dos
cifras significativas si la primera de ellas es un 1, o si siendo la primera un
2, la segunda no llega 5. En todos los demás casos debe darse un valor con una
sola cifra, 3 aumentando la primera en una unidad si la segunda fuera 5 o mayor
que 5. El valor de la magnitud debe tener sólo las cifras necesarias para que
su última cifra significativa sea del mismo orden decimal que la última del
error absoluto, llamada cifra de
acotamiento.
Como ejemplo damos la
siguiente tabla de valores de distintas magnitudes (en la columna de la izquierda mal escritos y
en la derecha corregidos) para poner de manifiesto lo dicho anteriormente.
Valores
Incorrectos Valores Correctos
3.418 ± 0.123
6.3 ± 0.09
46288 ± 1551
428.351 ± 0.27
0.01683
± 0.0058
Si un valor de medida es
leído de una tabla u otro lugar, sin indicación de su error, se tomara como
error una unidad del orden de la última cifra con que se expresa.
DETERMINACIÓN DE LOS
ERRORES COMETIDOS EN LAS MEDIDAS DIRECTAS
Cuando realicemos la
medida de cualquier magnitud deberemos indicar siempre una
estimación del error
asociado a la misma. Dado que no conocemos el valor "verdadero" de la
magnitud que deseamos
medir, se siguen ciertos procedimientos para hacer una estimación tanto del valor
"verdadero" de la magnitud, como de una cota de error, que nos
indique la incertidumbre en la determinación realizada.
Distinguiremos dos casos bien diferenciados:
a) Caso en el que se
realiza una única medida de una magnitud.
En este caso
consideramos que el error absoluto coincide con el valor de la sensibilidad del
aparato utilizado para
realizar la medida. De este modo el resultado de una medida lo indicaremos en la forma:
x ± Δx
(Δx = sensibilidad)
b) Caso en el que se
realizan varias medidas de una misma magnitud.
Con el fin de alcanzar
cierta validez estadística en los resultados de las medidas, es muy
conveniente repetir
varias veces la determinación del valor de la magnitud problema. Los resultados de las medidas
individuales pueden presentarse poco o muy dispersas, en función de esta
dispersión será conveniente
aumentar o no, el número de determinaciones del valor de la magnitud.
DETERMINACIÓN DEL ERROR DE UNA MAGNITUD MEDIDA INDIRECTAMENTE
La medida indirecta de una magnitud se alcanza por aplicación de una fórmula a un conjunto
de medidas directas, (variables independientes o datos), que las relacionan con la magnitud
problema. Mediante dicha fórmula se obtiene también el error de la medida según pasamos a
explicar. Antes de continuar, debemos indicar que si en dicha fórmula aparecen números
irracionales tales como pi, e, etc., debemos elegir el número de cifras significativas con que deben tomarse a la hora de realizar los cálculos correspondientes, de modo que los errores cometidos al aproximar estos números irracionales no afecten a la magnitud del error absoluto de la magnitud que queremos determinar.
Supongamos que la magnitud F es función de otras magnitudes físicas, estando relacionada
con ellas por F = f ( x, y, z, ...). Supongamos además, que se han realizado medidas de las citadas
variables, x, y, z...; y se han determinado su valor y su error. Para realizar el cálculo del error
absoluto de F, en función de los errores absolutos cometidos en las determinaciones directas de x, y,z.
En este problema se presenta una notable simplificación en el caso en el que la función
considerada sea de la forma:
F = x [exp(a)] ,y [exp(b)], z [exp(c)]...
"Las matemáticas pueden ser definidas como aquel tema del cual no sabemos nunca lo que decimos ni si lo que decimos es verdadero".
Bertrand Russell (1872-1970) Filósofo, matemático y escritor británico..
Bibliografía:
1. Fernández, S. (1997). Interlengua y análisis de
errores: en el aprendizaje del español como lengua extranjera. Madrid: Edelsa.
2. Santos Gargallo, I. (1993). Análisis contrastivo, análisis de
errores e interlengua en el marco de la lingüística contrastiva. Madrid: Síntesis.
1. Corder,
S. P. (1967). «The Significance of Learners'
Errors». En IRAL, 5,
pp. 161-170, recogido en Corder, S. P. (1981). Error Analysis and Interlanguage. Oxford: Oxford University Press.