SERIE DE TAYLOR

SERIE DE TAYLOR

teorema de Taylor: recibe su nombre del matemático británico Brook Taylor, quien lo enunció con mayor generalidad en 1712, aunque previamente James Gregory lo había descubierto en 1671. Este teorema permite obtener aproximaciones polinómicas de una función en un entorno de cierto punto en que la función sea diferenciable. Además el teorema permite acotar el error obtenido mediante dicha estimación.Este teorema permite aproximar una función derivable en el entorno reducido alrededor de un punto a: Є (a, d) mediante un polinomio cuyos coeficientes dependen de las derivadas de la función en ese punto.

La función p(x)=a₀+a₁x+a₂x²+..........+a_nxⁿ, en la que los coeficientes a_k son constantes, se llama polinomio de grado n. En particular y=ax+b es un polinomio de primer grado e y=ax²+bx+c es un polinomio de segundo grado. Los polinomios pueden considerarse las funciones más sencillas de todas. Para calcular su valor para una x dada, necesitamos emplear únicamente las operaciones de adición, sustracción y multiplicación; ni siquiera la división es necesaria. Los polinomios son funciones continuas para todo x y tienen derivadas de cualquier orden. Además la derivada de un polinomio es también un polinomio de grado inferior en una unidad, y las derivadas de orden n+1 y superiores de un polinomio de grado n son nulas.

Si a los polinomios añadimos las funciones de la forma y=p(x)/q(x) (cociente de polinomios, para cuyo cálculo necesitamos también de la división), las funciones raíz cuadrada de x y raíz cúbica de x, y finalmente, las combinaciones aritméticas de los tipos anteriores, obtenemos esencialmente las funciones cuyos valores pueden calcularse.

¿Qué es?

La serie de Taylor es una serie funcional y surge de una ecuación en la cual se puede encontrar una solución aproximada a una función.

¿Para que sirve?

La serie de Taylor proporciona una buena forma de aproximar el valor de una función en un punto en términos del valor de la función y sus derivadas en otro punto.

Por supuesto, para hacer esta aproximación sólo se pueden tomar unas cuantas expresiones de esta serie, por lo que el resto resulta en un error conocido como el término residual, es a criterio del que aplica la serie en numero de términos que ha de incluir la aproximación.

Pueden resolver por aproximación funciones trigonométricas, exponenciales, logarítmicas etc...

Esta representación tiene tres ventajas importantes:

• La derivación e integración de una de estas series se puede realizar término a término, que resultan operaciones triviales.
• Se puede utilizar para calcular valores aproximados de la función.
• Es posible demostrar que, si es viable la transformación de una función a una serie de Taylor, es la óptima aproximación posible.

Algunas funciones no se pueden escribir como serie de Taylor porque tienen alguna singularidad. En estos casos normalmente se puede conseguir un desarrollo en serie utilizando potencias negativas de x.

 

¿Cómo funciona?

La serie de Taylor se basa en ir haciendo operaciones según una ecuación general y mientras mas operaciones tenga la serie mas exacto será el resultado que se esta buscando. Dicha ecuación es la siguiente:

o expresado de otra forma

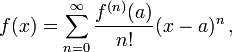
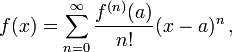
Donde n! es el factorial de n

F⁽ⁿ⁾ es la enésima derivada de f en el punto a

Como se puede observar en la ecuación, hay una parte en la cual hay que desarrollar un binomio (x-a) ⁿ por lo que para simplificar el asunto se igualara a "a" siempre a 0. Para fines prácticos no afecta mucho en el resultado si se hacen muchas operaciones en la serie.

Teorema: Si la función f y sus primeras n+1 derivadas son continuas en un intervalo que contiene a a y a x, entonces el valor de la función en un punto x está dado por:

La expansión en series de Taylor de n-ésimo orden debe ser exacta para un polinomio de n-ésimo orden.

Para otras funciones continuas diferenciables, como las exponenciales o sinusoidales, no se obtiene una estimación exacta mediante un número finito de términos.

El valor práctico de las series de Taylor radica en el uso de un número finito de términos que darán una aproximación lo suficientemente cercana a la solución verdadera para propósitos prácticos.

¿Cuántos términos se requieren para obtener una “aproximación razonable”?

La ecuación para el término residual se puede expresar como:

Rn= 0(hⁿ⁺¹)

Significa que el error de truncamiento es de orden hⁿ⁺¹. El error es proporcional al tamaño del paso h elevado a la (n+1)-ésima potencia.

Existen series de Taylor para:

• Función exponencial
• Logaritmo natural

 Serie Geométrica

Teorema del binomio

Funciones trigonométricas:

• Seno
• Coseno
• Tangente
• Secante
• Arco seno
• Arco tangente

Funciones hiperbólicas:

• Senh
• Cosh
• Tanh
• Senh-1
• Tanh-1

 Algunas de las mas utilizadas son las siguientes:

1.- Aproximación de la función y = sen (x)

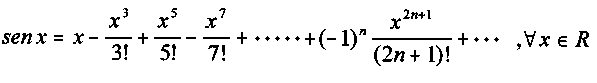
2.-Aproximación de la función y = cos (x)

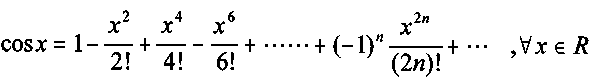
3.-Aproximación de la función y = e^x

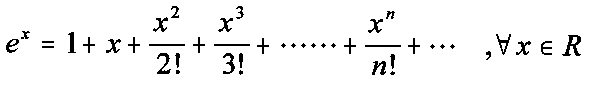
4.-Aproximación de la función y = ln (1+x)

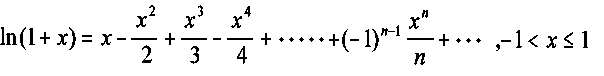
EJEMPLO:

 Uso de la expansión en serie de Taylor para aproximar una función con un número infinito de derivadas.

Utilizar los términos de la serie de Taylor con n= 0 hasta 6 para aproximar la función f(x) = cos(x) en x_i+1 = p/3 y sus derivadas en x_i = p/4. Esto significa que h = p/3- p/4 = p/12, los valores de las derivadas y el error de aproximación se presenta en la siguiente tabla.

Orden n	fn(x)	fn(p/4)	error (%)
0	cos(x)	0.707106781	-41.4
1	-sen(x)	0.521986659	-4.4
2	-cos(x)	0.497754491	0.449
3	sen(x)	0.499869147	2.62x10-2
4	cos(x)	0.500007551	-1.51x10-3
5	-sen(x)	0.500000304	-6.08x10-5
6	-cos(x)	0.499999988	2.40x10-6

Note, que a medida que se introducen más términos, la aproximación se vuelve más exacta y el porcentaje de error disminuye. En general podemos tener una aproximación polinomial de la función coseno, con sus derivadas en cero dada por

Orden n	fn(x)	fn(0)
0	cos(x)	1
1	-sen(x)	0
2	-cos(x)	-1
3	sen(x)	0
4	cos(x)	1
5	-sen(x)	0
6	-cos(x)	-1
7	sen(x)	0
8	cos(x)	1
9	-sen(x)	0
10	-cos(x)	-1

La aproximación polinomial final queda:

f(x)=  1-  1/2 x²  + 1/4!x⁴   – 1/6 x⁶+  1/8! x¹⁰+....

La implementación en Java es:

class funciones

{

  public static double coseno(double x)

  {

    int i;

    double s = 0;

    int signo = 1;

    for(i=0; i<10; i+=2)

    {

      s += signo*pow(x, i) / factorial(i);

      signo *= -1;

    }

    return s;

  }

  public static double seno(double x)

  {

    int i;

    double s = 0;

    int signo = 1;

    for(i=1; i<10; i+=2)

    {

      s += signo*pow(x, i) / factorial(i);

      signo *= -1;

    }

    return s;

  }

  public static double factorial(int x)

  {

    int i;

    double fact = 1;

    for(i=1; i<=x; i++)

      fact *= i;

    return fact;

  }

  public static double pow(double x, int n)

  {

    int i;

    double pow =1;

    if(x==0) return 0;

    for(i=1; i<=n; i++)

      pow = pow*x;

    return pow;

  }

}

El programa principal para realizar el llamado es:

public class ej053 {

  public static void main(String[] args) {

    int i,N;

    double inicio = -3.1416, fin = 3.1416, incremento = 0.1;

    N = (int)((fin - inicio)/incremento) + 1;

    double x[] = new double [N];

    double y[] = new double [N];

    double z[] = new double [N];

    for(i=0;  i<N; i++)

    {

      x[i] = inicio + incremento *i;

      y[i] = funciones.seno(x[i]);

      z[i] = funciones.coseno(x[i]);

    }

    grafica g = new grafica("Funcion seno");

    g.Datos(x,y);

    g.Datos(x,z);

    g.show();

  }

}

Note en este último código, el uso de la función gráfica que permite desplegar una función dada como dos arreglos de datos.

En matemáticas uno no entiende las cosas, se acostumbra a ellas.

John Von Neumann

Bibliografía :
http://lc.fie.umich.mx/~calderon/programacion/Mnumericos/STaylor.html
http://es.wikipedia.org/wiki/Serie_de_Taylor
http://www.tonahtiu.com/notas/metodos/serie_taylor.htm
http://www.unizar.es/analisis_matematico/analisis1/apuntes/09-seriespotencias.pdf
http://www.slideshare.net/Natalia1122/serie-de-taylor-4798773
http://www.ugr.es/~acanada/docencia/matematicas/historia/Taylor_Fourier.pdf
http://recursostic.educacion.es/descartes/web/materiales_didacticos/Desarrollo_serie_taylor/Desarrollo_en_serie_de_taylor.htm
http://www.frasesypensamientos.com.ar/frases-de-matematicas.html