Introducción al Análisis de Errores

A continuación definiremos algunos conceptos para así después poder comprender completamente el próximo tema.

Análisis:

Un análisis, en sentido amplio, es la descomposición de un todo en partes para poder estudiar su estructura, sistemas operativos, funciones, etc.

Error:

En general, se denomina error a todo juicio o valoración que contraviene el criterio que se reconoce como válido, en el campo al que se refiere el juicio.

En ciencias naturales y matemáticas:

§  Error experimental: la inexactitud cometida por culpa de no poder controlar adecuadamente la influencia de todas las variables presentes en un experimento.

§  Error de medición: la inexactitud que se acepta como inevitable al comparar una magnitud con su patrón de medida. El error de medición depende de la escala de medida empleada, y tiene un límite. Los errores de medición se clasifican en distintas clases (accidentales, aleatorios, sistemáticos, etc.).

§  Error de aproximación: es una medida del error cometido al aproximar una magnitud numérica por una expresión aproximada más sencilla que la expresión original exacta.

§  Error de cálculo: inexactitud o equivocación al realizar una operación matemática.

Numero:

Un número, en ciencia, es un concepto que expresa una cantidad en relación a su unidad. También puede indicar el orden de una serie (números ordinales). También, en sentido amplio, indica el carácter gráfico que sirve para representarlo, dicho signo gráfico de un número recibe el nombre de numeral o cifra. El que se escribe con un solo guarismo se llama dígito.

En matemática moderna, el concepto de número incluye abstracciones tales como números fraccionarios, negativos, irracionales, trascendentales, complejos(todos ellos con correlatos físicos claros) y también números de tipo más abstractos como los números hipercomplejos que generalizan el concepto de número complejo o los números hiperreales, los súper reales y los surreales que incluyen a los números reales como subconjunto.

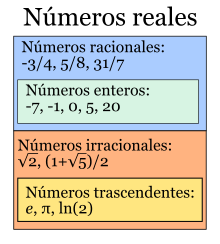
Números Reales:

En matemáticas, los números reales (designados por R) incluyen tanto a los números racionales (positivos y negativos y el cero) como a los números irracionales (trascendentes, algebraicos), que no se pueden expresar de manera fraccionaria y tienen infinitas cifras decimales no periódicas. 

Los números reales pueden ser descritos y construidos de varias formas, algunas simples aunque carentes del rigor necesario para los propósitos formales de matemáticas y otras más complejas pero con el rigor necesario para el trabajo matemático formal.

Durante los siglos XVI y XVII el cálculo avanzó mucho aunque carecía de una base rigurosa, puesto que en el momento no se consideraba necesario el formalismo de la actualidad, y se usaban expresiones como «pequeño», «límite», «se acerca» sin una definición precisa. Esto llevó a una serie de paradojas y problemas lógicos que hicieron evidente la necesidad de crear una base rigurosa para la matemática, la cual consistió de definiciones formales y rigurosas (aunque ciertamente técnicas) del concepto de número real.¹ En una sección posterior se describirán dos de las definiciones precisas más usuales actualmente: clases de equivalencia de sucesiones de Cauchy de números racionales y cortaduras de Dedekind.

Recta real.

Número imaginario: 

En matemáticas, un número imaginario es un número complejo cuya parte real es igual a cero, por ejemplo:  es un número imaginario, así como o  o   son también números imaginarios. En otras palabras, es un número de la forma:

 en donde 

Convencionalmente, se le llama imaginario puro, o simplemente imaginario, si el contexto no se presta a confusión; de otro modo, los términos número imaginario y número complejo quieren decir lo mismo.

Un número imaginario puro puede describirse como el producto de un número real por la unidad imaginaria i, en donde la letra i denota la raíz cuadrada de -1 (-1 ().).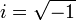

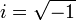Fue en el año 1777 cuando Leonhard Euler le dio a  el nombre de i, por imaginario, de manera despectiva dando a entender que no tenían una existencia real. Gottfried Leibniz, en el siglo XVII, decía que  era una especie de anfibio entre el ser y la nada.

En ingeniería electrónica y campos relacionados, la unidad imaginaria es a menudo escrita como j para evitar la confusión con la intensidad de una corriente eléctrica, tradicionalmente denotada por i.

Clasificación de números Complejos  Reales  Racionales  Enteros  Naturales  Naturales primos Naturales compuestos Cero Enteros negativos Fraccionarios Fracción propia Fracción impropia Irracionales Irracionales algebraicos Trascendentes Imaginarios puros

Operación matemática:

En matemática una operación es la acción de un operador sobre los elementos de un conjunto. El operador toma los elementos iniciales y los relaciona con otro elemento de un conjunto final que puede ser de la misma naturaleza o no; esto se conoce técnicamente como ley de composición.

El conjunto de partida puede estar formado por elementos de un único tipo (las operaciones aritméticas actúan sólo sobre números) o de varios (el producto de un vector por un escalar engloba al conjunto unión de vectores y escalares que conforman un espacio vectorial).

Dependiendo de cómo sean los conjuntos implicados en la operación con respecto al conjunto considerado principal según nuestras intenciones podemos clasificar las operaciones en dos tipos: internas y externas.

Resultado:

v Efecto de un hecho, operación o razonamiento: hice todas las gestiones posibles, pero no conseguí ningún resultado.

v Solución de una operación matemática.

v Información conseguida después de una operación o investigación: los resultados de los análisis fueron buenos.

v Tanteo de una competición deportiva: les ofrecemos los resultados de los partidos jugados.

Algoritmo:

Podemos encontrar muchas definiciones completas o formales de algoritmo en los textos de algorítmica y programación, todas ellas muy similares:

a) Secuencia finita de instrucciones, reglas o pasos que describen de forma precisa las operaciones de un ordenador debe realizar para llevar a cabo un tarea en un tiempo más finito. [Donald E. Knuth, 1968]

b)Descripción de un esquema de comportamiento expresado mediante un reportorio finito de acciones y de informaciones elementales, identificadas, bien comprendidas y realizables a priori. Este repertorio se denomina léxico [Pierre Scholl, 1988]

c)Un algoritmo es un conjunto finito de pasos definidos, estructurados en el tiempo y formulados con base a un conjunto finito de reglas no ambiguas, que proveen un procedimiento para dar la solución o indicar la falta de esta a un problema en un tiempo determinado. [Rodolfo Quispe-Otazu, 2004].

Características:

Las características fundamentales que debe cumplir todo algoritmo son:

§  Ser definido: Sin ambigüedad, cada paso del algoritmo debe indicar la acción a realizar sin criterios de interpretación.

§  Ser finito: Un número específico y numerable de pasos debe componer al algoritmo, el cual deberá finalizar al completarlos.

§  Tener cero o más entradas: Datos son proporcionados a un algoritmo como insumo (o estos son generados de alguna forma) para llevar a cabo las operaciones que comprende.

§  Tener una o más salidas: Debe siempre devolver un resultado; de nada sirve un algoritmo que hace algo y nunca sabemos que fue. El devolver un resultado no debe ser considerado como únicamente “verlos” en forma impresa o en pantalla, como ocurre con las computadoras. Existen muchos otros mecanismos susceptibles de programación que no cuentan con una salida de resultados de esta forma. Por salida de resultados debe entenderse todo medio o canal por el cual es posible apreciar los efectos de las acciones del algoritmo.

§  Efectividad: El tiempo y esfuerzo por cada paso realizado debe ser preciso, no usando nada más ni nada menos que aquello que se requiera para y en su ejecución.

Programación: 

Es el proceso de diseñar, codificar, depurar y mantener el código fuente de programas computacionales. El código fuente es escrito en un lenguaje de programación. El propósito de la programación es crear programas que exhiban un comportamiento deseado. El proceso de escribir código requiere frecuentemente conocimientos en varias áreas distintas, además del dominio del lenguaje a utilizar, algoritmos especializados y lógica formal. Programar no involucra necesariamente otras tareas tales como el análisis y diseño de la aplicación (pero sí el diseño del código), aunque sí suelen estar fusionadas en el desarrollo de pequeñas aplicaciones.

Lenguaje de programación:

 Es un idioma artificial diseñado para expresar computaciones que pueden ser llevadas a cabo por máquinas como las computadoras. Pueden usarse para crear programas que controlen el comportamiento físico y lógico de una máquina, para expresar algoritmos con precisión, o como modo de comunicación humana.¹ Está formado por un conjunto de símbolos y reglas sintácticas y semánticas que definen su estructura y el significado de sus elementos y expresiones. Al proceso por el cual se escribe, se prueba, se depura, se compila y se mantiene el código fuente de un programa informático se le llama programación.

También la palabra programación se define como el proceso de creación de un programa de computadora, mediante la aplicación de procedimientos lógicos, a través de los siguientes pasos:

§El desarrollo lógico del programa para resolver un problema en particular.

§Escritura de la lógica del programa empleando un lenguaje de programación específico (codificación del programa).

§Ensamblaje o compilación del programa hasta convertirlo en lenguaje de máquina.

§  Prueba y depuración del programa.

§  Desarrollo de la documentación.

v Variables y Vectores:

Las variables podrían calificarse como contenedores de datos y por ello se diferencian según el tipo de dato que son capaces de almacenar. En la mayoría de lenguajes de programación se requiere especificar un tipo de variable concreto para guardar un dato concreto. Por ejemplo, en Java, si deseamos guardar una cadena de texto deberemos especificar que la variable es del tipo "String". Por contra en otros lenguajes como PHP, este tipo de especificación de variables no es necesario. Además también existen variables compuestas por varias variables llamados vectores. Un vector no es más que un conjunto de variables ordenadas guardadas dentro de una variables contenedor del tipo vector. A continuación añadimos un listado con los tipos de variables y vectores más comunes:

§ Variables tipo Char: Estas variables contienen un único carácter, es decir, una letra, un signo o un número.

§  Variables tipo Int: Contienen un número entero.

§  Variables tipo float: Contienen un número decimal.

§  Variables tipo String: Contienen cadenas de texto, o lo que es lo mismo, es un vector con varias variables del tipo Char.

§  Variables del tipo Boolean: Solo pueden contener un 0 o un 1. El cero es considerado para muchos lenguajes como la variable del tipo String "False" mientras que el 1 se considera "True".

v Condicionantes:

Los condicionantes son estructuras de código que indican que para que cierta parte del programa se ejecute deben cumplirse ciertas premisas, como por ejemplo, que dos valores sean iguales, que un valor exista, que un valor sea mayor que otro y similares. Estos condicionantes por lo general solo se ejecutan una vez a lo largo del programa

v Bucles:

Los bucles son parientes cercanos de los condicionantes, pero ejecutan constantemente un código mientras se cumpla una determinada condición.

v Funciones:

Las funciones se crearon para evitar tener que repetir constantemente fragmentos de código. Una función podría considerarse como una variable que encierra código dentro de si. Por tanto cuando accedemos a dicha variable (la función) en realidad lo que estamos es diciendo al programa que ejecute un determinado código predefinido anteriormente.

Todos los lenguajes de programación tienen algunos elementos de formación primitivos para la descripción de los datos y de los procesos o transformaciones aplicadas a estos datos (tal como la suma de dos números o la selección de un elemento que forma parte de una colección). Estos elementos primitivos son definidos por reglas sintácticas y semánticas que describen su estructura y significado respectivamente.

v Sintaxis:

A la forma visible de un lenguaje de programación se le conoce como sintaxis. La mayoría de los lenguajes de programación son puramente textuales, es decir, utilizan secuencias de texto que incluyen palabras, números y puntuación, de manera similar a los lenguajes naturales escritos. Por otra parte, hay algunos lenguajes de programación que son más gráficos en su naturaleza, utilizando relaciones visuales entre símbolos para especificar un programa.

La implementación:

La implementación de un lenguaje es la que provee una manera de que se ejecute un programa para una determinada combinación de software y hardware. Existen básicamente dos maneras de implementar un lenguaje: compilación e interpretación.

v Compilación: es el proceso que traduce un programa escrito en un lenguaje de programación a otro lenguaje de programación, generando un programa equivalente que la máquina será capaz interpretar. Los programas traductores que pueden realizar esta operación se llaman compiladores. Éstos, como los programas ensambladores avanzados, pueden generar muchas líneas de código de máquina por cada proposición del programa fuente.

v Interpretación: es una asignación de significados a las fórmulas bien formadas de un lenguaje formal. Como los lenguajes formales pueden definirse en términos puramente sintácticos, sus fórmulas bien formadas pueden no ser más que cadenas de símbolos sin ningún significado. Una interpretación otorga significado a esas fórmulas.

"Nada ocurre porque si. Todo en la vida es una sucesión de hechos que, bajo la lupa del análisis, responden perfectamente a causa y efecto". 

Richard Feynmann

Bibliografia:
http://maths.anu.edu.au/~rennie/Analysis
http://www1.unex.es/eweb/fisteor/santos/mma/libro.metodos.matematicos.avanzados.2006.
http://es.wikipedia.org/wiki/N%C3%BAmero_imaginario
http://wmatem.eis.uva.es/~matpag/CONTENIDOS/Reales
http://www.mailxmail.com
http://www.profesorenlinea.cl/matematica