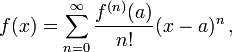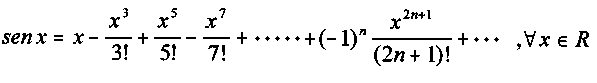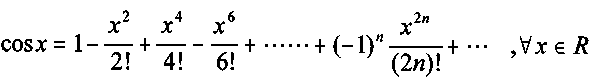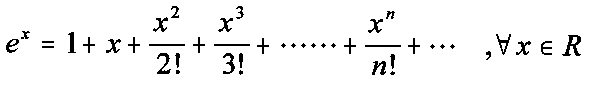Software "Gratis y Libre".

Ciudadan@ de internet.

Software Gratis y Libre.

Encuentre los programas gratis para su computadora, ya sea para uso privado o profesional.

Autor: Ángel Gutiérrez, David Zurdo, Ramón Montero.

Editorial: Alfaomega.

Introducción:

Mediante el progreso del internet, se han establecido muchas aplicaciones que ahora están a nuestra disposición. En este libro se habla de algunas de ellas, unas gratuitas y otras de prueba.

La forma  mas normal en las que se presentan los programas que es posible descargar de internet es la de un archivo, que consiste en la instalación.

Por ejemplo no es raro que un archivo se encuentre comprimido por lo cual en este libro podeos encontrar programas para l des- comprensión, ya que  estos programas son de los mas requeridos para la descarga de un archivo.

Los archivos a descargar pueden encontrarse en el propio servidor del desarrollador de la aplicación, o bien en otros servidores en principio autorizados por el, que reciben el nombre de servidores de replica o mirrors.

Sea cual se la fuente de descarga es recomendable siempre que sea posible un chequeo de las aplicaciones después de descargarlas, tanto con un programa de antivirus  como con u programa anti spyware.

Otra medida de seguridad general muy conveniente es asegurarse dela originalidad e integridad del archivo descargado.

Metaproducts download expres

Este se trata de una herramienta que hace capas el reinicio de descargas que hallan sido detenidas por causas fortuitas es decir, en las que halla ávido un corte repentino de corriente, una caída de conexión a internet, etc. O que hallan sido canceladas temporalmente por el usuario, para completarlas en otro momento.

Todos estos problemas te los evita este programa ya que el administrador de descargas de Explorer es muy limitado.

Descarga e instalación http://www.metaproducts.com y valla a la imagen con el texto download Express free power by MassDounloader.y después download.

HashCalc

con este programa es posible verificar la firma de las aplicaciones descargadas en aquellas donde dicha firma venga indicada. Este programa permite comprobar una gran cantidad de algoritmos distintos como el MD, el SHA, y diversas variantes, el PANAMA, EL TIGRE, o los algoritmos utilizados por Emule  o Edoney.

Descarga e instalación http://www.slavasoft.com y agá clic en hashcal.y en seguida download.

WinRAR

Es un compresor excelente capaz de descomprimir un buen numero de formatos distintos, incluidos los mas habituales como ZIP,ARJ, y ACE. Y es capas de descomprimir también su propio formato a demás de ZIP.

Funciones básica:

Des - comprensión de un archivo:

Una vez instalado el programa para acceder a las opciones de descompresión de un archivo o de una carpeta RAR o de cualquier formato compatible, basta hacer clic sobre el botón derecho del ratón. Hay varias alternativas pero la mas general es extraer archivo con la que el RAR se descomprimirá en la ruta que usted indique mediante un explorador de disco con el nombre que usted lo establezca.

Compresión de un archivo:

Si lo que pretende es comprimir un  archivo una carpeta basta que de un clic sobre el  con el botón derecho del ratón. La opción más general en este caso es añadir el archivo mediante la que podrá  indicar la ruta y nombre del archivo o carpeta  a comprimir. Tenga en cuenta que cuanto mejor sea la comprensión mas pequeño será el archivo comprimido, pero mas tiempo llevara en comprimirlo.

Descarga e instalación http://winrar,com.es y agá clic en descargas y pulse descargas recomendadas, su nombre actual es wrar361es.exe y finalmente de de instalar.

AVG free edition

Es este es un antivirus gratuito, pero de prestigio y fiabilidad reconocido. De hecho, su versión de pago, AVG PRO, se considera hoy en día por los expertos uno de los diez mejores sistemas antivirus del mundo lo que supone sin lugar a dudadas una buena garantía.

 Descarga e instalación:

Acceda a la pagina http://free.grisoft.com. Luego pulse en el enlace AVG antivirus Free. Después valla a la función load free versión. De clic sobre el y ira a la pagina de descarga propiamente dicha. Haga clic en el nombre de archivo EXE para que comience la descarga.

Con este programa podrá escanear completamente su equipo, escanear parcialmente, escanear un archivo y dar protección permanente.

Bitdefender

Este programa es seguramente el mejor, el mas rápido y mas eficaz antivirus del mundo. Cuenta con una interfaz muy sencilla de utilizar y ofrece la posibilidad de actualizaciones automáticas.

Este programa se encuentra disponible en español y existe una versión de evaluación que puede descargarse de internet funciona durante un periodo de 30 días.

Descarga e instalación:

Entre en la dirección http://www.bitdefenderes.com/index.php, y en la lista de la izquierda agá clic en el enlace descargas- versiones de evaluación. Elija BitDefender Antivirus Plus v10 y oprima el botón enviar.

Con este programa podrá analizar a profundidad, llevar el analis completo del sistema, análisis rápido, análisis de unidades extraíbles, análisis en la  memoria, analizar en busca de rootkits,etc.

Spybot Search & Destroy

Es un programa que se encarga de eliminar los spyware, es decir este programa es un anti- spyware.

Descarga en www.safernetworking.org/es/download/index.html

Spy sweeper:

Programa anti spyware/adware, que previene efectos nocivos y la presencia de efectos nocivos derivados de la instalación y presencia de aplicaciones de espías o publicitarias.

Este programa es de prueba pero esta en español.

Descarga e instala:www.webroot.com/es/products/spysweeper y agá clic en probarlo.

CCleaner

es un programa gratuito que protege la privacidad de los usuarios. Es el caso de herramientas que permiten, por ejemplo eliminar completamente y de modo definido el historial de la paginas web visitadas.

Descarga e instalación:

 http://www.ccleaner.com/ccdownload.asp y de clik en el enlace Download from FileHippo.Com y después de clik en le enlace download lastest versión.

Picasa

Este programa en español y ofrecido gratuitamente por el celebre buscador de google, es una especia de álbum digital que permite la ordenación y la clasificación de las imágenes del equipo a de mas ofrece otras posibilidades interesantes.

Descarga e instancian http://picasa.google.com

Nero

Se determina una suite multimedia. Se trata de un excelente programa constituido por una serie de programas unido a una interfaz. Por ejemplo esos módulos permiten  grabar un CD o DVD, crear caratulas, editar archivos de sonido, etc.

Ofrece una versión completa, gratuita y en español, funcional por un tiempo limitado.

Descarga e instalación http://www.nero.com/nero7/esp/nero7demo.php

winAvi

Maneja soportes y formatos de distintos audios y video con los objetivos de transformar unos formatos en potros rápido, sencillo, y eficaz distintos formatos de video entre si.

Es en ingles y por un periodo limitado.

Descarga e instalación http://www.winavi.com/en/download/download.htm y agá clic sobre winAvi.

Babylon

Es un potente diccionario bidireccional español – ingles, que cuenta además con herramientas adicionales muy prácticas como la búsqueda de sinónimos y antónimos o la conversación de unidades de distintos tipos.

Esta en español y ofrece una versión de prueba por tiempo limitado.

Descarga e instalación http://www.babylon.com/index.php y agá clic en le boto que dice pruebe babylon.

Bootvis

Es una herramienta que permite reducir al mínimo el tiempo de carga del sistema y la diferencia con le tiempo normal puede ser  muy considerable.

Descarga e instalación http://www.ma.jorgeeks.com/download.php?det=664

Comentario:

Este libro realmente es muy útil ya que te describe detalladamente para que sirve cada uno de los programas, además que estos son gratuitos, algunos solo son de evaluación y por tiempo limitado pero la gran mayoría no. La ventaja de esto es que te da un par de opciones para elegir el programa que mas te agrade o te parezca mas útil ya que menciona dos o mas programas para un fin común.

Aparte ya no tienes que estar buscándolos en la red ya que te da la pagina y además te dice como descargarlo e instalarlo detalladamente para que puedas tener una descarga rápida fácil y eficaz.

Los programas que menciona van desde programas de entretenimiento, protección, organizadores, convertidores gráficos, así como programas que nos ayudaran mucho académicamente como son los software para la compresión y des compresión, convertidores de formatos y diccionarios, entre otros, o para hacer cualquier tipo de actividad, puesto engloba una muy amplia rama de categorías.

Lo que me gusto es de que además de que te da todas las herramientas para que tengas un buen equipo, te dice en que idioma viene y cuanto puede llegar a durar, sin mencionar el lenguaje que maneja que es fácil de entender.

SERIE DE TAYLOR

SERIE DE TAYLOR

teorema de Taylor: recibe su nombre del matemático británico Brook Taylor, quien lo enunció con mayor generalidad en 1712, aunque previamente James Gregory lo había descubierto en 1671. Este teorema permite obtener aproximaciones polinómicas de una función en un entorno de cierto punto en que la función sea diferenciable. Además el teorema permite acotar el error obtenido mediante dicha estimación.Este teorema permite aproximar una función derivable en el entorno reducido alrededor de un punto a: Є (a, d) mediante un polinomio cuyos coeficientes dependen de las derivadas de la función en ese punto.

La función p(x)=a₀+a₁x+a₂x²+..........+a_nxⁿ, en la que los coeficientes a_k son constantes, se llama polinomio de grado n. En particular y=ax+b es un polinomio de primer grado e y=ax²+bx+c es un polinomio de segundo grado. Los polinomios pueden considerarse las funciones más sencillas de todas. Para calcular su valor para una x dada, necesitamos emplear únicamente las operaciones de adición, sustracción y multiplicación; ni siquiera la división es necesaria. Los polinomios son funciones continuas para todo x y tienen derivadas de cualquier orden. Además la derivada de un polinomio es también un polinomio de grado inferior en una unidad, y las derivadas de orden n+1 y superiores de un polinomio de grado n son nulas.

Si a los polinomios añadimos las funciones de la forma y=p(x)/q(x) (cociente de polinomios, para cuyo cálculo necesitamos también de la división), las funciones raíz cuadrada de x y raíz cúbica de x, y finalmente, las combinaciones aritméticas de los tipos anteriores, obtenemos esencialmente las funciones cuyos valores pueden calcularse.

¿Qué es?

La serie de Taylor es una serie funcional y surge de una ecuación en la cual se puede encontrar una solución aproximada a una función.

¿Para que sirve?

La serie de Taylor proporciona una buena forma de aproximar el valor de una función en un punto en términos del valor de la función y sus derivadas en otro punto.

Por supuesto, para hacer esta aproximación sólo se pueden tomar unas cuantas expresiones de esta serie, por lo que el resto resulta en un error conocido como el término residual, es a criterio del que aplica la serie en numero de términos que ha de incluir la aproximación.

Pueden resolver por aproximación funciones trigonométricas, exponenciales, logarítmicas etc...

Esta representación tiene tres ventajas importantes:

• La derivación e integración de una de estas series se puede realizar término a término, que resultan operaciones triviales.
• Se puede utilizar para calcular valores aproximados de la función.
• Es posible demostrar que, si es viable la transformación de una función a una serie de Taylor, es la óptima aproximación posible.

Algunas funciones no se pueden escribir como serie de Taylor porque tienen alguna singularidad. En estos casos normalmente se puede conseguir un desarrollo en serie utilizando potencias negativas de x.

 

¿Cómo funciona?

La serie de Taylor se basa en ir haciendo operaciones según una ecuación general y mientras mas operaciones tenga la serie mas exacto será el resultado que se esta buscando. Dicha ecuación es la siguiente:

o expresado de otra forma

Donde n! es el factorial de n

F⁽ⁿ⁾ es la enésima derivada de f en el punto a

Como se puede observar en la ecuación, hay una parte en la cual hay que desarrollar un binomio (x-a) ⁿ por lo que para simplificar el asunto se igualara a "a" siempre a 0. Para fines prácticos no afecta mucho en el resultado si se hacen muchas operaciones en la serie.

Teorema: Si la función f y sus primeras n+1 derivadas son continuas en un intervalo que contiene a a y a x, entonces el valor de la función en un punto x está dado por:

La expansión en series de Taylor de n-ésimo orden debe ser exacta para un polinomio de n-ésimo orden.

Para otras funciones continuas diferenciables, como las exponenciales o sinusoidales, no se obtiene una estimación exacta mediante un número finito de términos.

El valor práctico de las series de Taylor radica en el uso de un número finito de términos que darán una aproximación lo suficientemente cercana a la solución verdadera para propósitos prácticos.

¿Cuántos términos se requieren para obtener una “aproximación razonable”?

La ecuación para el término residual se puede expresar como:

Rn= 0(hⁿ⁺¹)

Significa que el error de truncamiento es de orden hⁿ⁺¹. El error es proporcional al tamaño del paso h elevado a la (n+1)-ésima potencia.

Existen series de Taylor para:

• Función exponencial
• Logaritmo natural

 Serie Geométrica

Teorema del binomio

Funciones trigonométricas:

• Seno
• Coseno
• Tangente
• Secante
• Arco seno
• Arco tangente

Funciones hiperbólicas:

• Senh
• Cosh
• Tanh
• Senh-1
• Tanh-1

 Algunas de las mas utilizadas son las siguientes:

1.- Aproximación de la función y = sen (x)

2.-Aproximación de la función y = cos (x)

3.-Aproximación de la función y = e^x

4.-Aproximación de la función y = ln (1+x)

EJEMPLO:

 Uso de la expansión en serie de Taylor para aproximar una función con un número infinito de derivadas.

Utilizar los términos de la serie de Taylor con n= 0 hasta 6 para aproximar la función f(x) = cos(x) en x_i+1 = p/3 y sus derivadas en x_i = p/4. Esto significa que h = p/3- p/4 = p/12, los valores de las derivadas y el error de aproximación se presenta en la siguiente tabla.

Orden n	fn(x)	fn(p/4)	error (%)
0	cos(x)	0.707106781	-41.4
1	-sen(x)	0.521986659	-4.4
2	-cos(x)	0.497754491	0.449
3	sen(x)	0.499869147	2.62x10-2
4	cos(x)	0.500007551	-1.51x10-3
5	-sen(x)	0.500000304	-6.08x10-5
6	-cos(x)	0.499999988	2.40x10-6

Note, que a medida que se introducen más términos, la aproximación se vuelve más exacta y el porcentaje de error disminuye. En general podemos tener una aproximación polinomial de la función coseno, con sus derivadas en cero dada por

Orden n	fn(x)	fn(0)
0	cos(x)	1
1	-sen(x)	0
2	-cos(x)	-1
3	sen(x)	0
4	cos(x)	1
5	-sen(x)	0
6	-cos(x)	-1
7	sen(x)	0
8	cos(x)	1
9	-sen(x)	0
10	-cos(x)	-1

La aproximación polinomial final queda:

f(x)=  1-  1/2 x²  + 1/4!x⁴   – 1/6 x⁶+  1/8! x¹⁰+....

La implementación en Java es:

class funciones

{

  public static double coseno(double x)

  {

    int i;

    double s = 0;

    int signo = 1;

    for(i=0; i<10; i+=2)

    {

      s += signo*pow(x, i) / factorial(i);

      signo *= -1;

    }

    return s;

  }

  public static double seno(double x)

  {

    int i;

    double s = 0;

    int signo = 1;

    for(i=1; i<10; i+=2)

    {

      s += signo*pow(x, i) / factorial(i);

      signo *= -1;

    }

    return s;

  }

  public static double factorial(int x)

  {

    int i;

    double fact = 1;

    for(i=1; i<=x; i++)

      fact *= i;

    return fact;

  }

  public static double pow(double x, int n)

  {

    int i;

    double pow =1;

    if(x==0) return 0;

    for(i=1; i<=n; i++)

      pow = pow*x;

    return pow;

  }

}

El programa principal para realizar el llamado es:

public class ej053 {

  public static void main(String[] args) {

    int i,N;

    double inicio = -3.1416, fin = 3.1416, incremento = 0.1;

    N = (int)((fin - inicio)/incremento) + 1;

    double x[] = new double [N];

    double y[] = new double [N];

    double z[] = new double [N];

    for(i=0;  i<N; i++)

    {

      x[i] = inicio + incremento *i;

      y[i] = funciones.seno(x[i]);

      z[i] = funciones.coseno(x[i]);

    }

    grafica g = new grafica("Funcion seno");

    g.Datos(x,y);

    g.Datos(x,z);

    g.show();

  }

}

Note en este último código, el uso de la función gráfica que permite desplegar una función dada como dos arreglos de datos.

En matemáticas uno no entiende las cosas, se acostumbra a ellas.

John Von Neumann

Bibliografía :
http://lc.fie.umich.mx/~calderon/programacion/Mnumericos/STaylor.html
http://es.wikipedia.org/wiki/Serie_de_Taylor
http://www.tonahtiu.com/notas/metodos/serie_taylor.htm
http://www.unizar.es/analisis_matematico/analisis1/apuntes/09-seriespotencias.pdf
http://www.slideshare.net/Natalia1122/serie-de-taylor-4798773
http://www.ugr.es/~acanada/docencia/matematicas/historia/Taylor_Fourier.pdf
http://recursostic.educacion.es/descartes/web/materiales_didacticos/Desarrollo_serie_taylor/Desarrollo_en_serie_de_taylor.htm
http://www.frasesypensamientos.com.ar/frases-de-matematicas.html